Logistic Regression

在分类问题中，要预测的 $y$ 值离散的，逻辑回归是目前最流行使用最广泛的一种用于分类的学习算法。

Hypothesis

分类：$y = 0\ or\ 1$
在逻辑回归中，$0\ <\ h_\theta\ <1 $， $h_\theta = g(\theta^TX)$，其中$X$ 表示特征向量，$g(z)=\frac{1}{1+e^{-z}}$ 是一个常用的S型$(Sigmoid Function)$ 逻辑函数。

import numpy as np

# sigmoid function
def sigmoidFunc(z):
    return 1.0 / (1.0 + np.exp(-z))

# set axes
def originset():
    ax = plt.gca()
    ax.spines['right'].set_color('none')
    ax.spines['top'].set_color('none')
    ax.xaxis.set_ticks_position('bottom')
    ax.yaxis.set_ticks_position('left')
    ax.spines['bottom'].set_position(('data', 0))
    ax.spines['left'].set_position(('data', 0))

originset()

z = np.arange(-10, 10, 0.1)
plt.plot(x, sigmoidFunc(x), 'b')
plt.yticks(np.arange(0.2, 1.2, 0.2))
plt.title('$Sigmoid\ Function$')

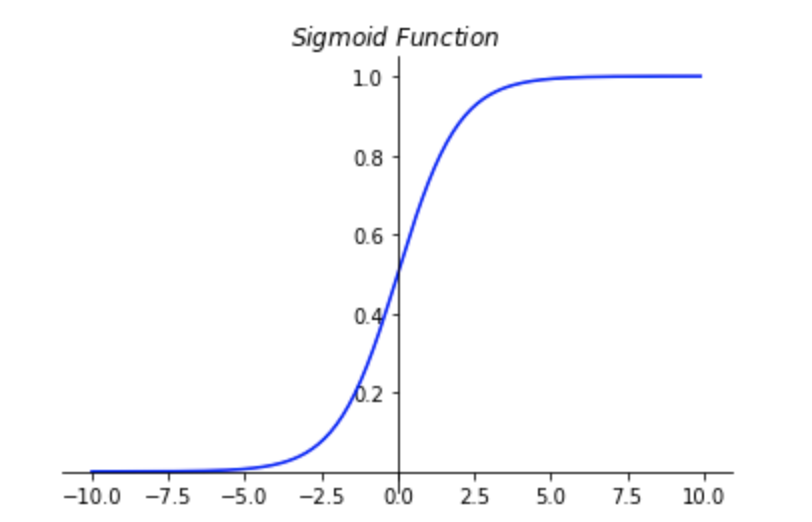
对$h_\theta$ 的理解：
1. 在逻辑回归中，当$h_\theta(x) >= 0.5$ 时，$y = 1$；当$h_\theta(x) < 0.5$ 时，$y = 0$。
2. 对于一个输入，根据选定的参数计算输出变量为1的可能性，即$h_{\theta}(x)=P(y=1 | x ; \theta)$。例如，如果对于给定的$x$，通过已经确定的参数计算得出$h_\theta(x) = 0.7$，则表示有$70\%$ 的几率$y$ 为正向类，相应地$y$ 为负向类的几率为$1-0.7=0.3$。

Cost Function

对于线性回归，可以使用模型误差的平方和作为代价函数$J(\theta)$，在此基础上最小化$J(\theta)$ 以求得$\theta $，此时的代价函数是一个凸函数，没有局部最小值，可以很容易的找到全局最小值。但对于逻辑回归模型来说，若按照这样的思路来定义代价函数，此时的代价函数是非凸函数，有就很多的局部极小值，不利于梯度下降法的求解。
于是需要根据逻辑回归的特征重新定义代价函数：$J(\theta)=\frac{1}{m} \sum_{i=1}^{m} \operatorname{cost}\left(h_{\theta}\left(x^{(i)}\right), y^{(i)}\right)$。其中
$$\begin{equation}
\operatorname{cost}\left(h_{\theta}(x), y\right)=\left{\begin{aligned}-\log \left(h_{\theta}(x)\right) & \text { if } y=1 \\-\log \left(1-h_{\theta}(x)\right) & \text { if } y=0 \end{aligned}\right.
\end{equation}$$
$h_\theta(x)$ 与$\operatorname{cost}\left(h_{\theta}\left(x^{(i)}\right), y^{(i)}\right)$ 的关系如下图所示：
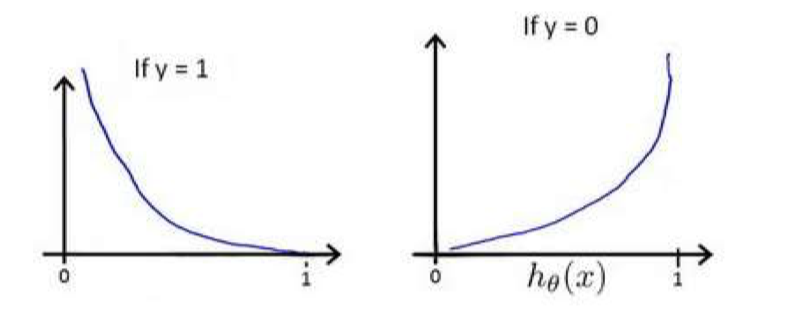
从上图可以看出$\operatorname{cost}\left(h_{\theta}\left(x^{(i)}\right), y^{(i)}\right)$ 的特点：当$y = 1$时，$h_\theta$ 越接近$1$，$\operatorname{cost}\left(h_{\theta}\left(x^{(i)}\right), y^{(i)}\right)$ 越小，反之越大；当$y = 0$时，$h_\theta$ 越接近 $0$，$\operatorname{cost}\left(h_{\theta}\left(x^{(i)}\right), y^{(i)}\right)$ 越小，反之越大。
根据这一特点，构建$\operatorname{cost}\left(h_{\theta}\left(x^{(i)}\right), y^{(i)}\right)$ 如下：$\operatorname{cost}\left(h_{\theta}(x), y\right)=-y \times \log \left(h_{\theta}(x)\right)-(1-y) \times \log \left(1-h_{\theta}(x)\right)$。

据此可得代价函数：$J(\theta)=\frac{1}{m} \sum_{i=1}^{m}\left[-y^{(i)} \log \left(h_{\theta}\left(x^{(i)}\right)\right)-\left(1-y^{(i)}\right) \log \left(1-h_{\theta}\left(x^{(i)}\right)\right)\right]$。


# cost function
def costfn(theta, X, y, mylambda = 0):
    term1 = np.dot(-y.T, np.log(h(theta, X)))
    term2 = np.dot((1 - y).T, np.log(1 - h(theta, X)))

# regularized term
regn = (mylambda/ (2.0 * m)) * np.sum(np.power(theta[1:], 2))
return float(1.0/m * np.sum(term1 - term2) + regn)

Gradient

在得到代价函数之后，我们便可以利用梯度下降法来求解使代价函数最小的参数$\theta$。

求解算法：Repeat $\theta_{j} :=\theta_{j}-\alpha \frac{\partial}{\partial \theta_{j}} J(\theta)$ and simultaneously update all $\theta_j$
求导后带入可得：Repeat $\theta_{j} :=\theta_{j}-\alpha \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(\mathrm{x}^{(i)}\right)-\mathrm{y}^{(i)} \quad\right) \mathrm{x}_{j}^{(i)} $ and simultaneously updata all $\theta_j$

Summary

主要公式：

Sigmoid function: $g(z)=\frac{1}{1+e^{-z}}$
Hypothesis: $h_\theta = g(\theta^TX) = g(z)=\frac{1}{1+e^{-\theta^TX}}$
$\operatorname{cost}:$ $\operatorname{cost}\left(h_{\theta}(x), y\right)=-y \times \log \left(h_{\theta}(x)\right)-(1-y) \times \log \left(1-h_{\theta}(x)\right)$
Cost function: $J(\theta)=\frac{1}{m} \sum_{i=1}^{m}\left[-y^{(i)} \log \left(h_{\theta}\left(x^{(i)}\right)\right)-\left(1-y^{(i)}\right) \log \left(1-h_{\theta}\left(x^{(i)}\right)\right)\right]$
Gradient: $\frac{\partial J(\theta)}{\partial \theta_{j}}=\frac{1}{m} \sum_{i=1}^{m}\left[h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right] x_{j}^{(i)}$

Appendix：the deviation of $J (\theta)$

$$J(\theta)=-\frac{1}{m} \sum_{i=1}^{m}\left[y^{(i)} \log \left(h_{\theta}\left(x^{(i)}\right)\right)+\left(1-y^{(i)}\right) \log \left(1-h_{\theta}\left(x^{(i)}\right)\right)\right]$$

由于$h_{\theta}\left(x^{(i)}\right)=\frac{1}{1+e^{-\theta^{T} x^{(i)}}}$，则：
$$\begin{array}{l}{y^{(i)} \log \left(h_{\theta}\left(x^{(i)}\right)\right)+\left(1-y^{(i)}\right) \log \left(1-h_{\theta}\left(x^{(i)}\right)\right)} \\ {=y^{(i)} \log \left(\frac{1}{1+e^{-\theta^{T} x^{(i)}}}\right)+\left(1-y^{(i)}\right) \log \left(1-\frac{1}{1+e^{-\theta^{T} x^{(i)}}}\right)} \\ {=-y^{(i)} \log \left(1+e^{-\theta^{T} x^{(i)}}\right)-\left(1-y^{(i)}\right) \log \left(1+e^{\theta^{T} x^{(i)}}\right)}\end{array}$$

所以，
$$\frac{\partial}{\partial \theta_{j}} J(\theta)=\frac{\partial}{\partial \theta_{j}}\left[-\frac{1}{m} \sum_{i=1}^{m}\left[-y^{(i)} \log \left(1+e^{-\theta^{T} x^{(i)}}\right)-\left(1-y^{(i)}\right) \log \left(1+e^{\theta^{T} x^{(i)}}\right)\right]\right]$$

$$\begin{array}{l}{=-\frac{1}{m} \sum_{i=1}^{m}\left[-y^{(i)} \frac{-x_{j}^{(i)} e^{-\theta^{T} x^{(i)}}}{1+e^{-\theta^{T} x^{(i)}}}-\left(1-y^{(i)}\right) \frac{x_{j}^{(i)} e^{\theta^{T} x^{(i)}}}{1+e^{\theta^{T} x^{(i)}}}\right]} \\ {=-\frac{1}{m} \sum_{i=1}^{m} y^{(i)} \frac{x_{j}^{(i)}}{1+e^{\theta^{T} x^{(i)}}}-\left(1-y^{(i)}\right) \frac{x_{j}^{(i)} e^{\theta^{T} x^{(i)}}}{1+e^{\theta^{T} x^{(i)}}} ]} \\ {=-\frac{1}{m} \sum_{i=1}^{m} \frac{y^{(i)} x_{j}^{(i)}-x_{j}^{(i)} e^{\theta^{T} x^{(i)}}+y^{(i)} x_{j}^{(i)} e^{\theta^{T} x^{(i)}}}{1+e^{\theta^{T} x^{(i)}}}} \\ {=-\frac{1}{m} \sum_{i=1}^{m} \frac{y^{(i)}\left(1+e^{\theta^{T} x^{(i)}}\right)-e^{\theta^{T} x^{(i)}}}{1+e^{\theta^{T} x^{(i)}}} x_{j}^{(i)}} \\ {=-\frac{1}{m} \sum_{i=1}^{m}\left(y^{(i)}-\frac{e^{\theta^{T} x^{(i)}}}{1+e^{\theta^{T} x^{(i)}}}\right) x_{j}^{(i)}} \\ {=-\frac{1}{m} \sum_{i=1}^{m}\left(y^{(i)}-\frac{1}{1+e^{-\theta^{T} x^{(i)}} )} x_{j}^{(i)}\right.} \\ {=-\frac{1}{m} \sum_{i=1}^{m}\left[y^{(i)}-h_{\theta}\left(x^{(i)}\right)\right] x_{j}^{(i)}} \\ {=\frac{1}{m} \sum_{i=1}^{m}\left[h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right] x_{j}^{(i)}}\end{array}$$
即
$$\frac{\partial J(\theta)}{\partial \theta_{j}}=\frac{1}{m} \sum_{i=1}^{m}\left[h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right] x_{j}^{(i)}$$

文章目录

Hypothesis

Cost Function

Gradient

Summary

Appendix：the deviation of $J (\theta)$